Storleks typ med Lucas sekvenser
Förhållandet mellan text och resten av en sida är en av de viktigaste egenskaperna hos en design.
Rytm, tonvikt och ton är alla komprometterade utan rätt skalad typ. Val av textstorlekar är emellertid ofta både en noggrann och frustrerande upplevelse, utan någon standardiserad utgångspunkt för att informera oss.
Som ett resultat hittar vi ofta webbdesigners som faller tillbaka på standardalternativen som presenteras av applikationer - 8pt, 10pt, 12pt, 14pt, 18pt - för att ha en bättre lösning.
Den bättre lösningen är att ställa in typstorlekar inte genom individuella infall, men enligt ett förutbestämt system; ett system som är enkelt att använda, praktiskt att implementera på webben och viktigast av allt, tillräckligt flexibelt för att ge designers ett komplett utbud av uttryck. Cue: Lucas-sekvensen.
Lucas sekvenser
Fibonacci Sequence - först inspelad i väst under 1200-talet av Leonardo Fibonacci - är följande uppsättning heltal (heltal):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ... ad infinitum
Sekvensen namngavs för Fibonacci av den framstående fransk matematiker François Édouard Lucas, den framstående 1800-talet, som producerade en liknande sekvens av hans egen, som han kallade Lucas Numbers:
2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843 ... ad infinitum
Fibonacci Sequence och Lucas Numbers är båda specifika variationer av den generiska Lucas Sequence.
Lucas Sekvenser och heltal sekvenser har i allmänhet varit föremål för en studieperiod för många fullbordade matematiker, så vi ska sammanfatta konceptet enligt följande:
- Vilket som helst tal i sekvensen är summan av de två föregående numren som beskrivs i denna formel: n = n-1 + n-2
- De två första siffrorna i sekvensen - kända som frönummer - väljs valfritt.
Varför använda en Lucas-sekvens för att sätta typ?
Lucas-sekvenser, i synnerhet i form av Fibonacci-sekvensen, har en nära relation till det gyllene förhållandet, vilket upprepas genom naturen i skal, spindelbanor, molnformationer och många andra naturliga underverk. Det finns starka bevis för att allt vi finner visuellt tilltalande beror på den formens förhållande till det gyllene förhållandet.
Viktigare är att Lucas Sequences ger oss en skalbar ram för inställning av typ som är både graciös och rytmisk.
Bestämning av vårt första frönummer
Det finns mycket debatt om rätt textstorlek för en webbplats. 12px är fortfarande den vanligaste, men det är inte ovanligt att se allt från 10px till 16px. Detta är väsentligt född av brist på förståelse för vad fontmått faktiskt betyder. Otroligt, för oss som är vana vid standardisering - eller åtminstone ambitioner om standardisering - finns det ingen standardmått i typdesign. två olika typdesigners, som ritar exakt samma design i typsnittsprogramvaran, kommer sannolikt att rita den i olika storlekar. Variationen mellan olika typsnitt är inte överraskande alldeles för vanligt.

Svaret på var du ska börja är smutsigt enkelt. Vår standardtextstorlek blir 1em, vilket betyder att vårt första frönummer kommer att vara 1.
Det finns ett antal viktiga fördelar med att använda 1em som vår utgångspunkt: Som en relativ måttenhet är en em väl lämpad för lyhörd design. genom att använda ems och multiplar av ems kan vi ändra storlek på hela vårt system genom att ändra basstorlekstorleken; äntligen är det en snygg begreppsmässig passform med vår Lucas-sekvens och kommer att tjäna till att påminna oss om den exakta heltalsekvensen om vi behöver återkomma till designen senare.
Det finns inget iboende fel med att använda procentandelar istället för ems, eller till och med pixlar eller punkter, men em är mer än sannolikt framtiden för webbdesign, så vi kan lika gärna vänja oss.
Bestämning av vårt andra frönummer
Det finns många strategier som är öppna för oss för att bestämma vårt andra frönummer. Vissa designers har en specifik preferens och skulle välja 1.2em eller liknande. Andra designers, som gillar mystiken i det gyllene förhållandet, kanske gillar att använda 1.618em.
En mer praktisk lösning är att bestämma det andra fröetallet med hjälp av linjehöjden på kroppstexten. Men eftersom linjens höjd vanligtvis dikteras av längden på linjen och linjelängden bestäms av ett rutnät är den mer lämpad att skriva ut eller inte-mottaglig webbdesign. Eftersom vi tittar på framtiden, och framtiden är lyhörd, fungerar den inte för oss.
Vad vi är kvar med, delvis genom en elimineringsprocess och delvis på grund av dess lämplighet, är typens x-höjd. Eller närmare bestämt förhållandet mellan x-höjden och resten av glyfen.
Ett kännetecken för bra design är upprepningen av nyckelelementen, och att bära proportionerna av typen till hela sidan är ett utmärkt tillfälle att både erkänna typdesigners arbete och införa vår design med en del av typsnittets karaktär.
Hitta vår x-höjd
För att hitta x-höjden på din typsnitt behöver vi öppna något som Photoshop eller Illustrator och lägga till lite text som innehåller en stigare (t.ex. "d") och bokstaven "x". Om du använder en bitmappsredigerare som Photoshop, sätt texten så stor som möjligt så att du får ett korrekt resultat. I dessa exempel har jag satt teckensnittet till 500pt för att mäta det.
Därefter mäta höjden från uppstigningslinjen till baslinjen och höjden från toppen av x till grundlinjen.
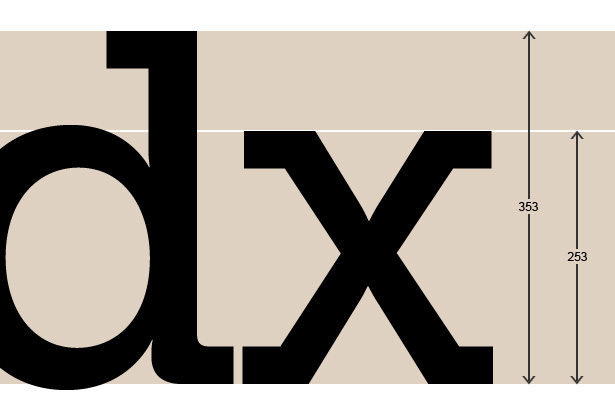
Självklart, om du har turen att få tillgång till bra typsnittsprogramvara, kan du helt enkelt öppna fontfilen som du ska använda och läsa av x-höjden och stigarens höjd.
Dela nu x-höjden med stigarens höjd för att hitta x-höjden i procent av hela:
x-höjd / uppstigningshöjd * 100 = andra frönummer
När det gäller teckensnittet i exemplet (vilket är Museo Slab) är resultatet:
253/353 = 0,71671388
eller 0,716em
Varför mäter vi inte från toppen av stigaren till botten av nedstigningen? Eftersom tecken inte tenderar att ha både en stigare och en descender (ett undantag är bokstaven "f") och följaktligen är relationerna inom formerna som består av typsnittets konstruktion baserade på förhållandet mellan x-höjden och en längre stam. Det är möjligt att mäta nedstigningen i stället, men eftersom kapphöjden (huvudets höjd) vanligtvis är mycket nära uppstigaren är det min preferens. Om du hittar dig själv med en typsnitt med en mer dominerande kvalitet - kontrasten i tjockleken på olika slag, till exempel - kanske du vill använda det värdet i stället för uppstigaren till x-höjdförhållandet.
Bestämningen av hur du kommer fram till ditt andra frönummer är ett av de viktigaste designbesluten du kommer att behöva göra, men det är inte något att agonize över; Välj ett nummer ur en hatt om du föredrar, och fortsätt, de goda grejerna är ännu inte kommande.
Det är värt att notera att om du byter ekvation runt och delar upp höjderhöjden med x-höjden kommer du att sluta med ett nummer som är större än ett. I så fall blir din sekvens brantare och lite mer dramatisk.
Skapa vår sekvens
Så, vi har våra två frönummer: 1em och 0.716em och vi har formeln n = n-1 + n-2:
1 + 0,716 = 1,716
0,716 + 1,716 = 2,432
1.716 + 2.432 = 4.148
etc.
Vilket resulterar i följande sekvens:
1, 0,716, 1,716, 2,432, 4,148, 6,58, 10,728, 17,308, 28,036 ... ad infinitum
Designbiten
Hittills har vi plockat oss igenom grundläggande, men användbar matematik, och vi har kommit fram till en sekvens som ger oss en rad storlekar från 1em till 28.036em och bortom om det behövs.
Vi kan nu använda dessa värden som våra typstorlekar i följd för att skapa ett välproportionerat typschema:

Du märker att vi börjar med p satt till 0.716 och h4 satt till 1, trots att det inte är sekventiellt korrekt. Anledningen är att i termer av hierarki är h4 viktigare än p. Vår Lucas Sequence får inte diktera hierarkin på sidan, det dikterar skalaförhållandena mellan olika element. Bara ditt innehåll kan diktera hierarkin .
Eftersom vi inte är begränsade till konsekutiva värden i vår sekvens och kan välja och välja vilka heltal vi använder, uppnår vi alltid rytm och struktur med samma sekvens. Även om vi tar ett mycket dramatiskt tillvägagångssätt:

Exakt samma Lucas-sekvens kan också användas för att skapa en mer reserverad, affärsliknande ordning:

Kärnan i detta system är att skalförhållandena bibehålls, hierarkin är proportionell, men det finns en stor mängd olika tillgängliga för konstruktören. Här ska du tjäna dina pengar: genom att välja storlekarna på skalan för att skapa hierarki och betoning.
Flexibilitet
Ofta dikteras typstorleken av mer än betoning: tillgänglighetsproblem uppstår om vi pratar om en publik med visuella svårigheter; den stora volymen av innehåll kan kasta upp begränsningar; Vi kan behöva vara flexibla - bokstavligen - när vi utformar en vätsklayout.
Lyckligtvis hanterar CSS med lätthet denna situation. Eftersom vi använder ems för våra storlekar kan vi ställa in vår typ med vår Lucas Sequence och sedan skala hela, genom att ställa in en standardstorlek på koden, behålla rytmen i vår design, men öka eller minska de faktiska värdena.

Observera i bilden att p, h2 och h1 storlekarna är desamma, alla ritade från vår sekvens. Det är variationen på teckensnittstorleken på kroppstaggen (0.8em till vänster och 1.4em till höger) som kaskader ner, vilket skapar radikalt olika resultat.
Till sist
Som beroende av underliggande matematik som detta system är, är det viktigt att erkänna att designen inte kan reduceras till en uppsättning ekvationer. Denna metod för dimensioneringstyp ger dig en struktur som du kan arbeta med, och hjälper dig att skapa välproportionerade typscheman, men det är som designer att använda systemet som ett verktyg, inte som en krycka.
Noterna och vågen i musik, även Jazz, kan reduceras till en uppsättning ekvationer som beskriver deras relation, men det tar någon som John Coltrane att få dessa relationer till liv.